
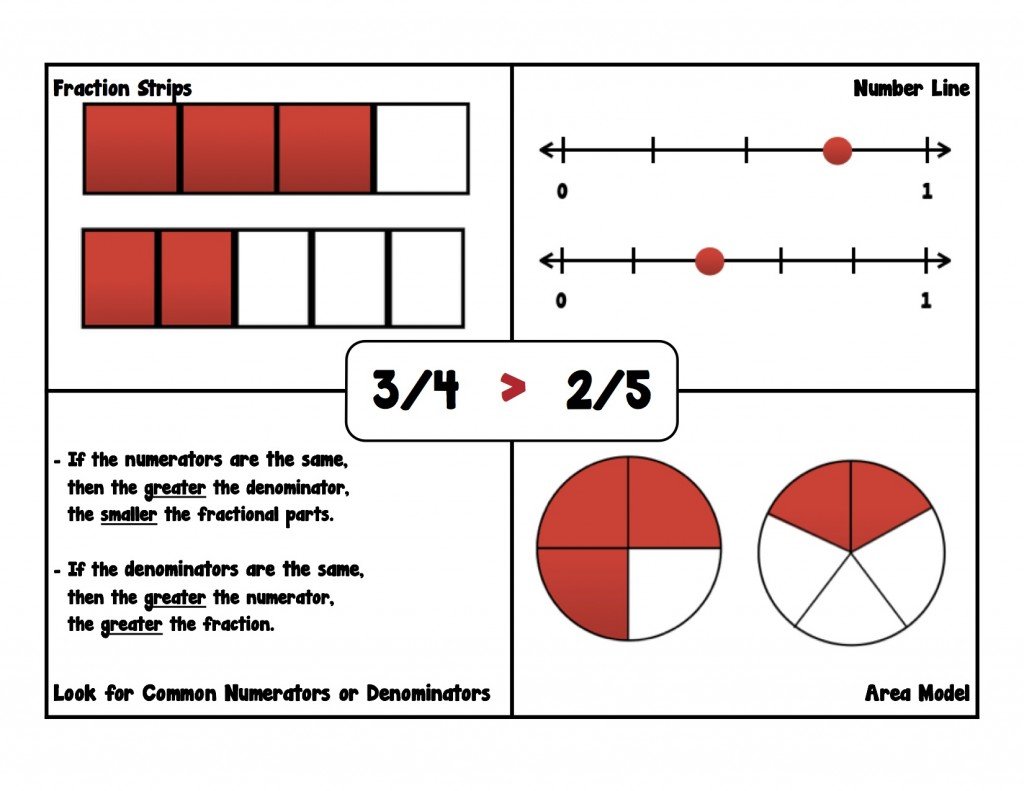
For instance, if we had the equationĦ × 4 = _, we could represent it like this: When we multiply whole numbers, we can represent the two factors in an array.
#Area models with fractions how to#
“Let’s review how to multiply whole numbers.
These models will allow you to explore the relationship between two fractions and their product.” “We will be using a paper-folding model and an area model to find the product of two fractions. The lesson focuses on proper fractions and not on improper fractions or mixed numbers. The goal of the lesson is for students to develop a conceptual understanding of the process of multiplying fractions by finding fractional parts of an area. Use the suggestions in the Extension section to tailor the lesson as needed. Other students may be pulled into a small group for additional instruction and guided practice. Students who understand the process may be given Station Cards to practice their skills. Use the Assessment Exit Ticket to evaluate student proficiency. Use question and answer to review the entire process with students using a large model (such as drawing on the board or a full-sized piece of paper) and walk through how to obtain the corresponding number sentence. Students gain experience by multiplying two fractions using the paper-folding technique, and then they write the corresponding number sentences. Point out that the product of two fractions results in a smaller number while the product of two whole numbers results in a larger number.
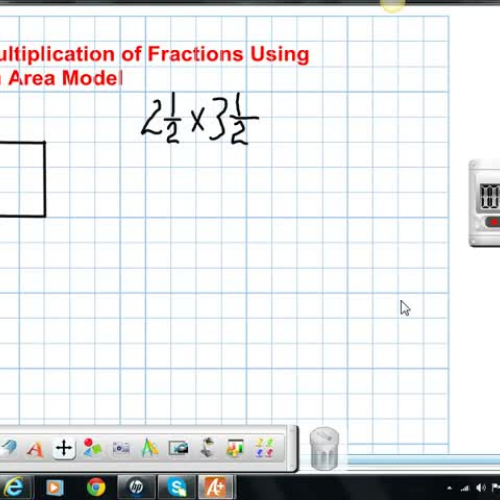

The focus of the lesson is on fractions, the multiplication of fractions, and the representation of fraction multiplication using physical models.ĭemonstrate how to visually represent fraction multiplication using paper-folding. Scaffolding, Active Engagement, Modeling, Explicit Instruction, Formative Assessment W:


 0 kommentar(er)
0 kommentar(er)
